角度がまとめられれて、 しかもそれが一直線上にあれば求めるのは簡単です。 一直線の角度とは、すなわち180度ですからね。 したがって 三角形の内角の和=180度 となるのです。三角関数の三角形への応用 ここからは、三角関数を利用した三角形の公式をまとめています。 正弦定理 三角形の3つの頂点を通る円はただ1つに決まり、これを外接円といいます。この外接円の半径を r として、次の正弦定理が成り立ちます。三角形には不思議な性質がたくさんあります。 その中にはまだ発見されていないものもあるはずです。 このジオジェブラを使うと正確な作図が簡単にでき、さらにアニメーションを使って変化を調べることができ、新しい発見が容易にできます。 「bもしかしたら・・・?

接弦定理の証明 円周角が直角ver 数学a By となりがトトロ マナペディア
円 三角形 角度 定理
円 三角形 角度 定理-(証明) 1 右のようにACが中心を通るとき oc=ob= (半径)だから OBCは二等辺三角形になる. 二等辺三角形の2つの底角は等しいから ∠ b= ∠ c (1) 「三角形の外角は,それと隣り合わない2つの内角の和に等しい」(重要定理)から,Contents 1 数学円周角の定理とは? 円と三角形による角度の定理、円周角と中心角の関係;


円周角の定理
三角関数の三角形への応用 ここからは、三角関数を利用した三角形の公式をまとめています。 正弦定理 三角形の3つの頂点を通る円はただ1つに決まり、これを外接円といいます。この外接円の半径を r として、次の正弦定理が成り立ちます。下の図のように円周上に15個の任意の点AからOをとり、1つおきに直線で結びました。角AからOまで15個の角の和は何度ですか。 → 解答 平面図形の角度の発展問題 問題1 下の図の三角形ABDと三角形ACEは正三角形です。Contents 1 数学円周角の定理とは? 円と三角形による角度の定理、円周角と中心角の関係;
接弦定理とは? 接弦定理とは、円に三角形が内接し、その頂点のどれか \(\bf{1}\) 点を通る円の接線があるときに、それらの 角度に関して成り立つ定理 です。方べきの定理は、実生活では等式そのものよりも「円と直線の交点 \(a,b,c,d,p,x\) によって作られる2組の三角形がそれぞれ相似である」ということが重要な定理です。 「どの三角形とどの三角形が相似なのか?方べきの定理は、実生活では等式そのものよりも「円と直線の交点 \(a,b,c,d,p,x\) によって作られる2組の三角形がそれぞれ相似である」ということが重要な定理です。 「どの三角形とどの三角形が相似なのか?
三角形の重心の性質 b 24 三角形の三中線は重心で交わり、重心は各中線 を2 1 に内分する ag∶gd=bg∶ge=cg∶gf=2∶1 21 円に内接する四角形の対角の和 a ab ch = 2 1 25 = 180° 22 円の共接線の長さ c ab=2√r×r 23 接弦定理a 頂角150°の二等辺三角形c三角形に関する大定理 三角形に関する定理は、山のようにあります。 そのなかでも、辺と角度の関係を表す式はいくつかありますが、 第2余弦定理こそが、それの真骨頂といえます。 この記事は、(第2) 余弦定理 の 覚え方 と 使い方 について書いています。 第2余弦定理三角形の各辺や角度を調べる時です。 大体の飛行機は高度1万メートルぐらいを飛行していますのと、地球の円も考慮して、0キロから300キロ先まで見えていたので、ビックリしました。 ピタゴラスの定理は知っていても、角度の計算となるとわから
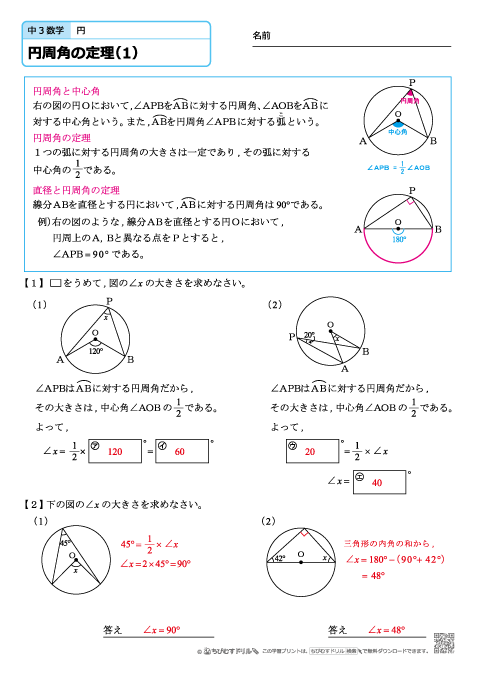


中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生



勉強しよう数学0 やさしい円周角の定理の覚え方
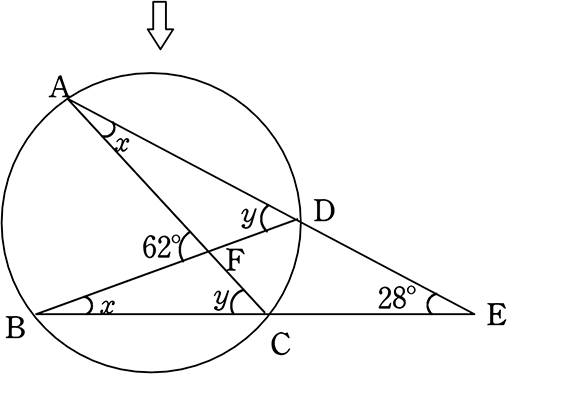
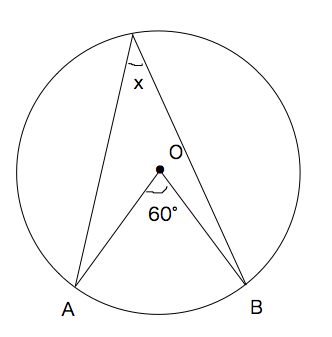
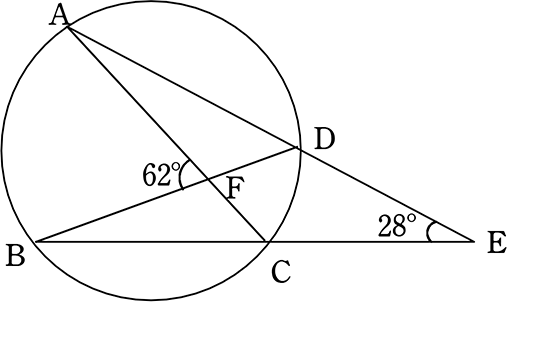
\(oa,ob,oc\)は全て円の半径だから、同じ長さになるね。 だから、\( oab, oac\)は二等辺三角形になります。 すると 二等辺三角形の底角は等しくなるから \(∠a\)の部分が25°と35°を合わせた60°になるということがわかります。円の中の図形の角度を求める入試問題の解説 円の中に描かれた図形の角度を求める高校入試過去問の解説です。 円周角の定理や三角形の性質、平行線と角など中学校の図形分野で 学ぶ知識を幅広く使わないと答えが出ない問題ばかりです。三角形の各辺や角度を調べる時です。 大体の飛行機は高度1万メートルぐらいを飛行していますのと、地球の円も考慮して、0キロから300キロ先まで見えていたので、ビックリしました。 ピタゴラスの定理は知っていても、角度の計算となるとわから



円周角の定理



中学数学 円周角 中心角
こんにちは。 da Vinch (@mathsouko_vinch)です。 正弦定理と外接円正弦定理を紹介した時に外接円については触れなかったので、ここで少し確認したいと思います。まず「外接円」とは何かというと三角形の3つの頂点全てを通るこの定理は「フォイエルバッハの定理」と呼ばれる、九点円に関する最も有名な定理のひとつである。 九点円と内接円の接点を フォイエルバッハ点 (英語版) と呼ぶ。 その他の性質 他に以下のような性質がある。 三角形の3個の頂点と垂心の4点からどの円に内接する四角形の向かい合う \(2\) 組の辺をそれぞれかけ算した合計が、 対角線の積と一致する という定理です。 トレミーの定理は、長方形で考えると理解しやすくなります。


円周角の定理は人生の縮図 円周角の定理が苦手な子どもへの処方箋 子どもの夢を叶える心理作戦
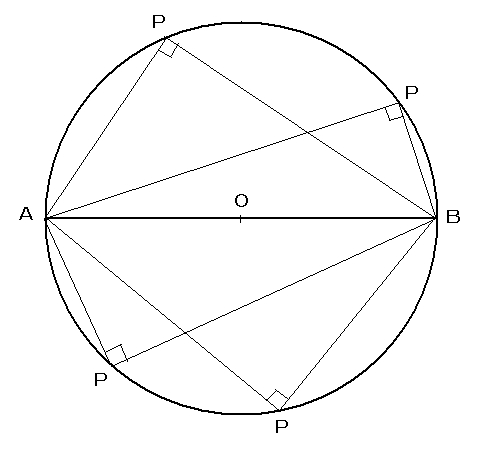


タレースの定理
三角形abcの外側に、中心oが来るイメージです。 このとき、円周角の定理を証明するには、 ∠bac=½ ∠boc を証明すればいいわけです。 今までと同じように、補助線を引き、同じ大きさの角度に印をつけていきます。(証明) 1 右のようにACが中心を通るとき oc=ob= (半径)だから OBCは二等辺三角形になる. 二等辺三角形の2つの底角は等しいから ∠ b= ∠ c (1) 「三角形の外角は,それと隣り合わない2つの内角の和に等しい」(重要定理)から,数学Aの円で使う定理・性質の一覧 円周角の定理 弧ABに対する円周角の大きさはつねに一定であり、その角の大きさは、その弧に対する中心角の大きさの半分である。 ・∠acb=∠adb ・∠aob=2∠acb=2∠adb また、次の図のよ
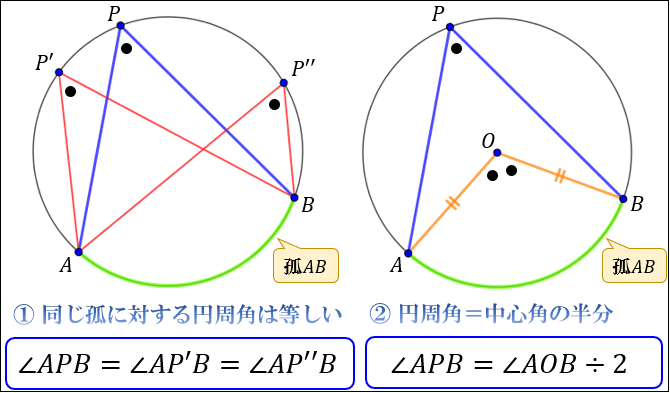


円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ


2番の解き方を教えてください 11 5 になります 中学数学円周角と中 Yahoo 知恵袋
以下のように、円の中心oを通る三角形 を考えます。 すると同位角の定理より、 となります。また、 は直角三角形なので が得れれます。 2 の場合 下記の図のようになり、半円がつくる円周角は90°なので となります。 3 の場合あとは「三角形の内角の和は \(180°\) 」「直線は \(180°\)」を使うと \(∠BAT=∠ACB\) となり、接弦定理を証明できました。 円の接線が接点を通る直径と垂直になる理由三角形に直線を引いて、二つの直角三角形となることがわかるのなら、どの角度にも三角比の値を定義して、問題はない。 正弦定理 三角形ABCかあって、 2つの頂点それぞれと向かい合う辺をx、y、z。 三角形の内接円の中心点から、それぞれの頂点に



円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ


円周角の定理
三角形の合同条件を使って、合同な三角形を見つける方法! 証明の書き方合同な三角形の証明問題の書き方を基礎から解説! 直角三角形証明問題の書き方とは?合同条件の使い方を徹底解説! 二等辺三角形の角度の求め方 厳選6問解説!2 円周角の定理の公式『中心角=円周角×2』が成り立つ理由、証明問題でも出題される? 21 ①三角形ABCの内側に円の中心Oがある場合:三角形と円の角度がいずれも鋭角以下のように、円の中心oを通る三角形 を考えます。 すると同位角の定理より、 となります。また、 は直角三角形なので が得れれます。 2 の場合 下記の図のようになり、半円がつくる円周角は90°なので となります。 3 の場合


円周角



Xの角度の求め方を教えてください 円周角の定理を使う問題です Clear
三角形の重心の性質 b 24 三角形の三中線は重心で交わり、重心は各中線 を2 1 に内分する ag∶gd=bg∶ge=cg∶gf=2∶1 21 円に内接する四角形の対角の和 a ab ch = 2 1 25 = 180° 22 円の共接線の長さ c ab=2√r×r 23 接弦定理a 頂角150°の二等辺三角形c以下のように、円の中心oを通る三角形 を考えます。 すると同位角の定理より、 となります。また、 は直角三角形なので が得れれます。 2 の場合 下記の図のようになり、半円がつくる円周角は90°なので となります。 3 の場合2 円周角の定理の公式『中心角=円周角×2』が成り立つ理由、証明問題でも出題される? 21 ①三角形ABCの内側に円の中心Oがある場合:三角形と円の角度がいずれも鋭角



円周角の定理の基本 計算 無料で使える中学学習プリント



6本の缶を最短の紐で束ねる意外な方法とは 円と球の不思議な雑学 横山 明日希 ブルーバックス 講談社 1 4
三角形の重心の性質 b 24 三角形の三中線は重心で交わり、重心は各中線 を2 1 に内分する ag∶gd=bg∶ge=cg∶gf=2∶1 21 円に内接する四角形の対角の和 a ab ch = 2 1 25 = 180° 22 円の共接線の長さ c ab=2√r×r 23 接弦定理a 頂角150°の二等辺三角形c三角形の合同条件を使って、合同な三角形を見つける方法! 証明の書き方合同な三角形の証明問題の書き方を基礎から解説! 直角三角形証明問題の書き方とは?合同条件の使い方を徹底解説! 二等辺三角形の角度の求め方 厳選6問解説!図形 定義・定理 まとめ 対頂角 𝟖は等しい 直線の角度 ° 平行線の 同位角 𝟖 は等しい 角形の内角の和 °×(𝒏− ) 平行線の 多角形の外角の和錯角 𝟔は等しい ° 同位角 が等しければ、2直線は平行 〇 合同な図形の対応する線分や角は等し



数学応用 円周角の定理 証明 中学生 数学のノート Clear



円による角度の求め方 中学数学に関する質問 勉強質問サイト
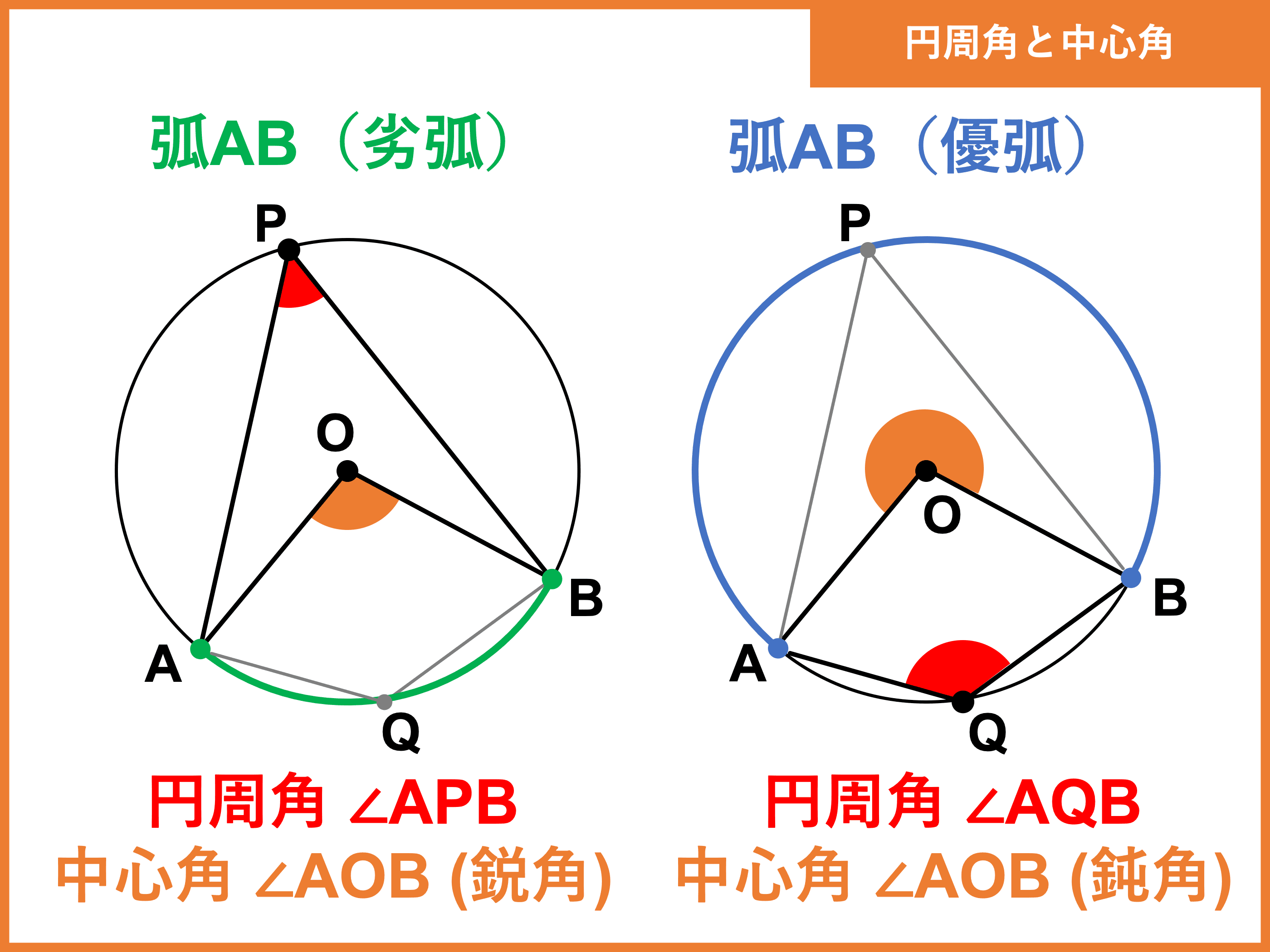


円周角の定理とは 定理の逆や証明 問題の解き方 受験辞典



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生
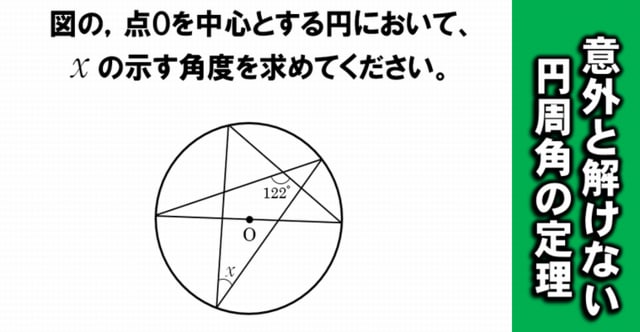


意外と解けない円周角の定理 中3レベルの数学問題 暇つぶしに動画で脳トレ
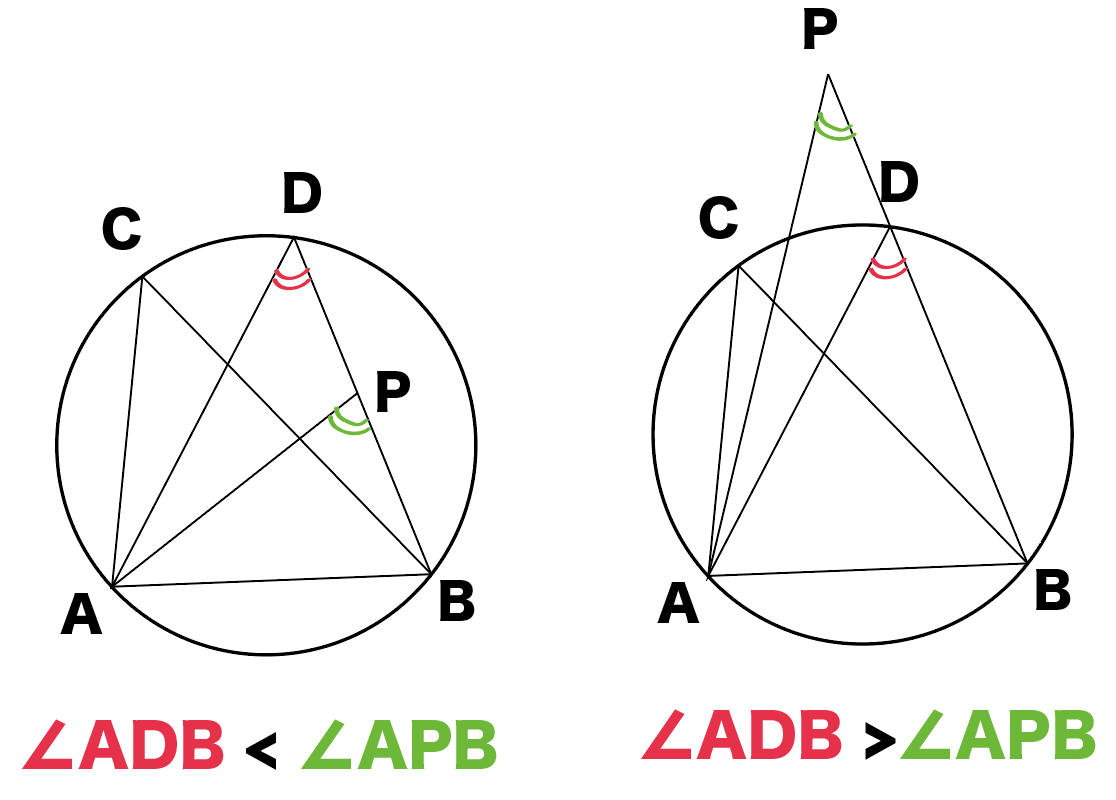


3分でわかる 円周角の定理の逆の証明 Qikeru 学びを楽しくわかりやすく
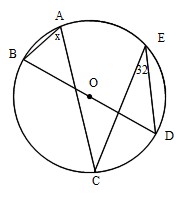


Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ
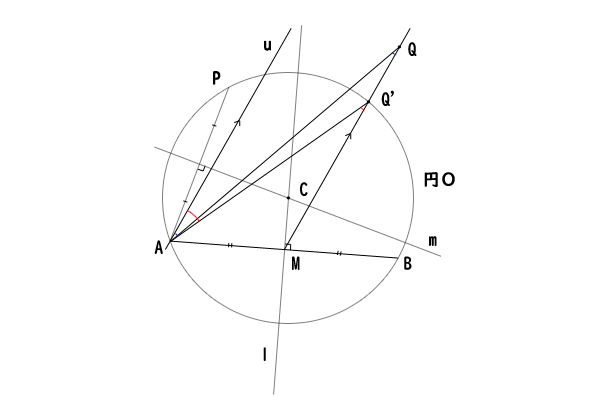


円周角の定理とその逆の証明 高校数学マスター



円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく
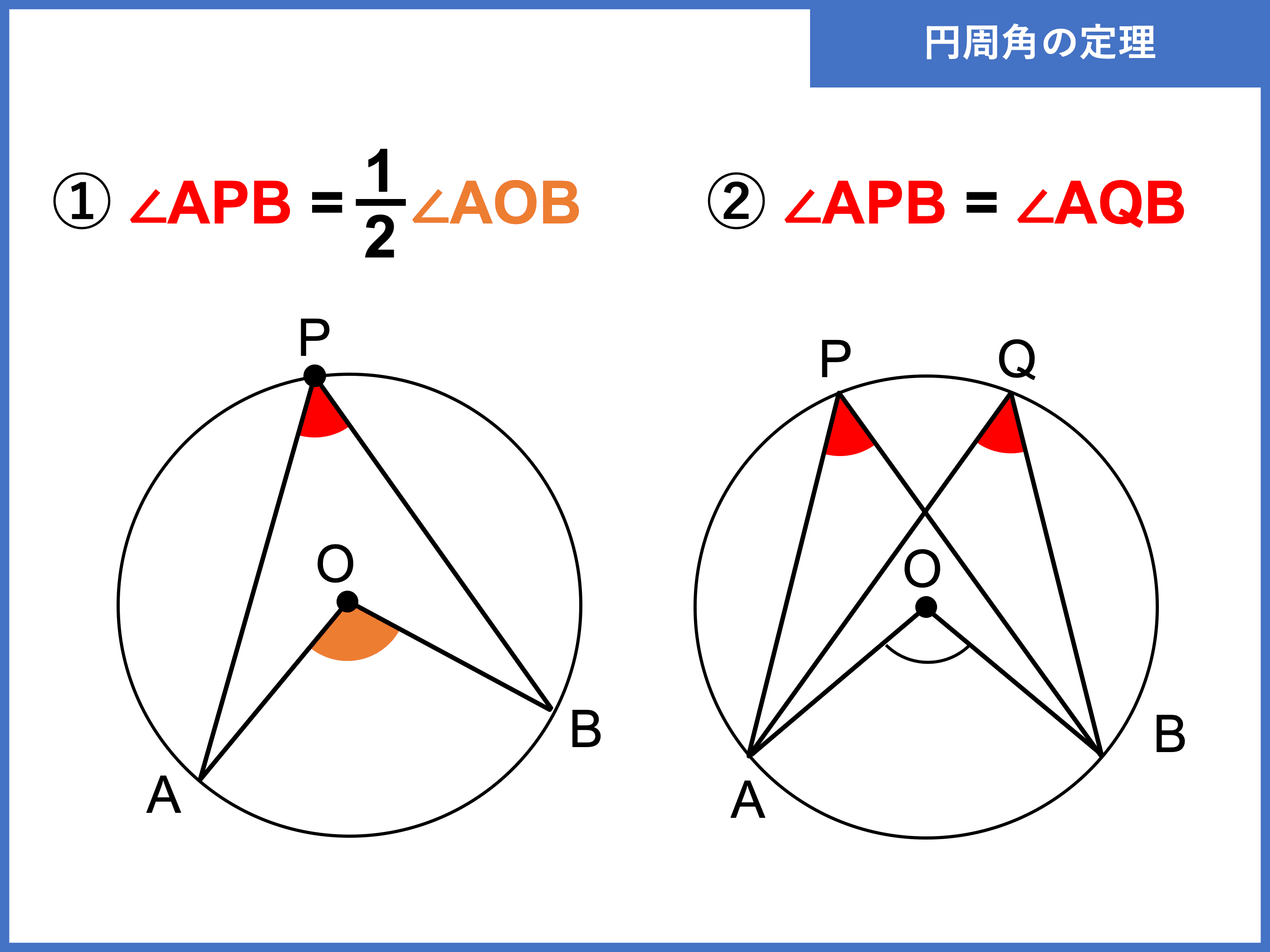


円周角の定理とは 定理の逆や証明 問題の解き方 受験辞典
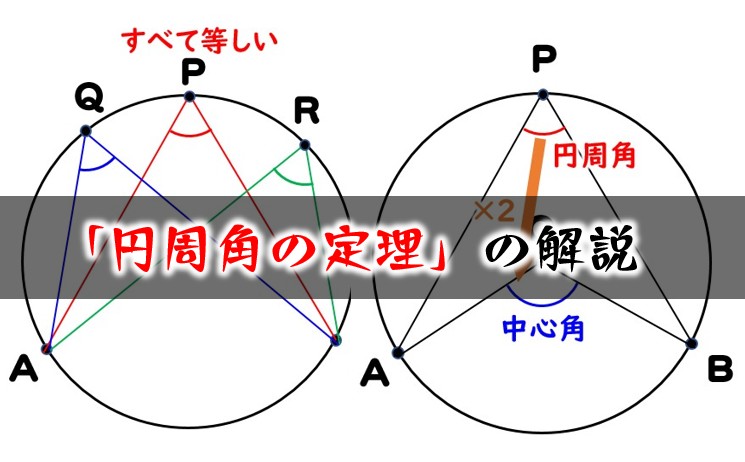


円周角の定理の解説 問題の解き方 数学fun



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ



円周角の定理の基本 計算 無料で使える中学学習プリント



円周角 中学数学に関する質問 勉強質問サイト



接弦定理の証明 円周角が直角ver 数学a By となりがトトロ マナペディア
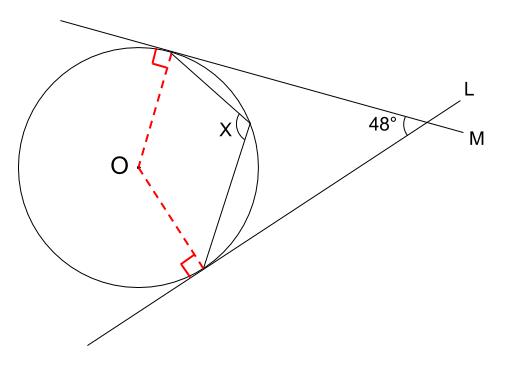


中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su



6本の缶を最短の紐で束ねる意外な方法とは 円と球の不思議な雑学 横山 明日希 ブルーバックス 講談社 1 4
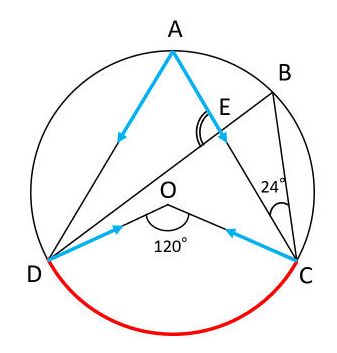


円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室
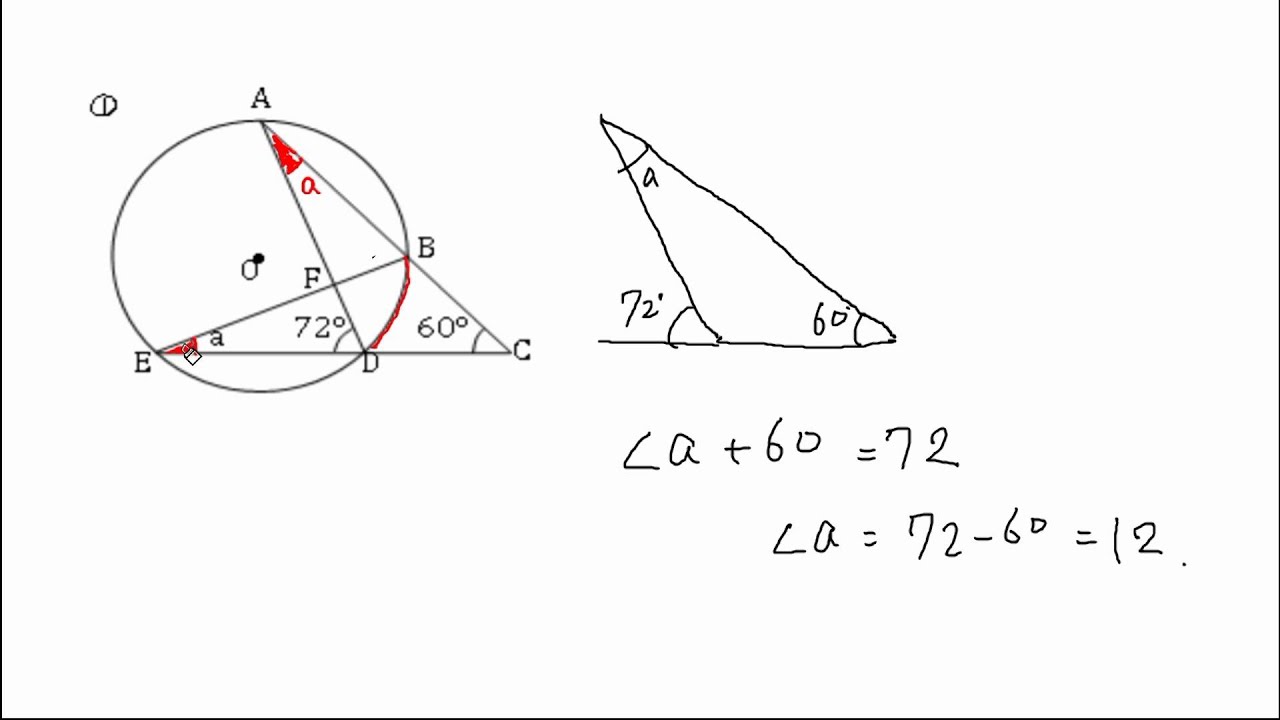


円周角の定理 問題 Youtube


内接円 内心
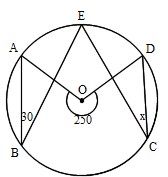


Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ



中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット



中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット
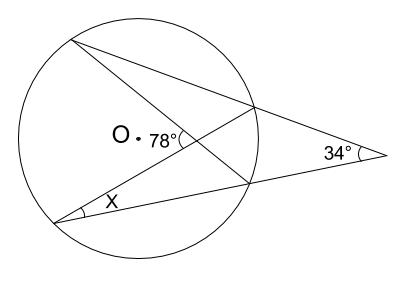


中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su



円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ



円周角の定理の逆 無料で使える中学学習プリント
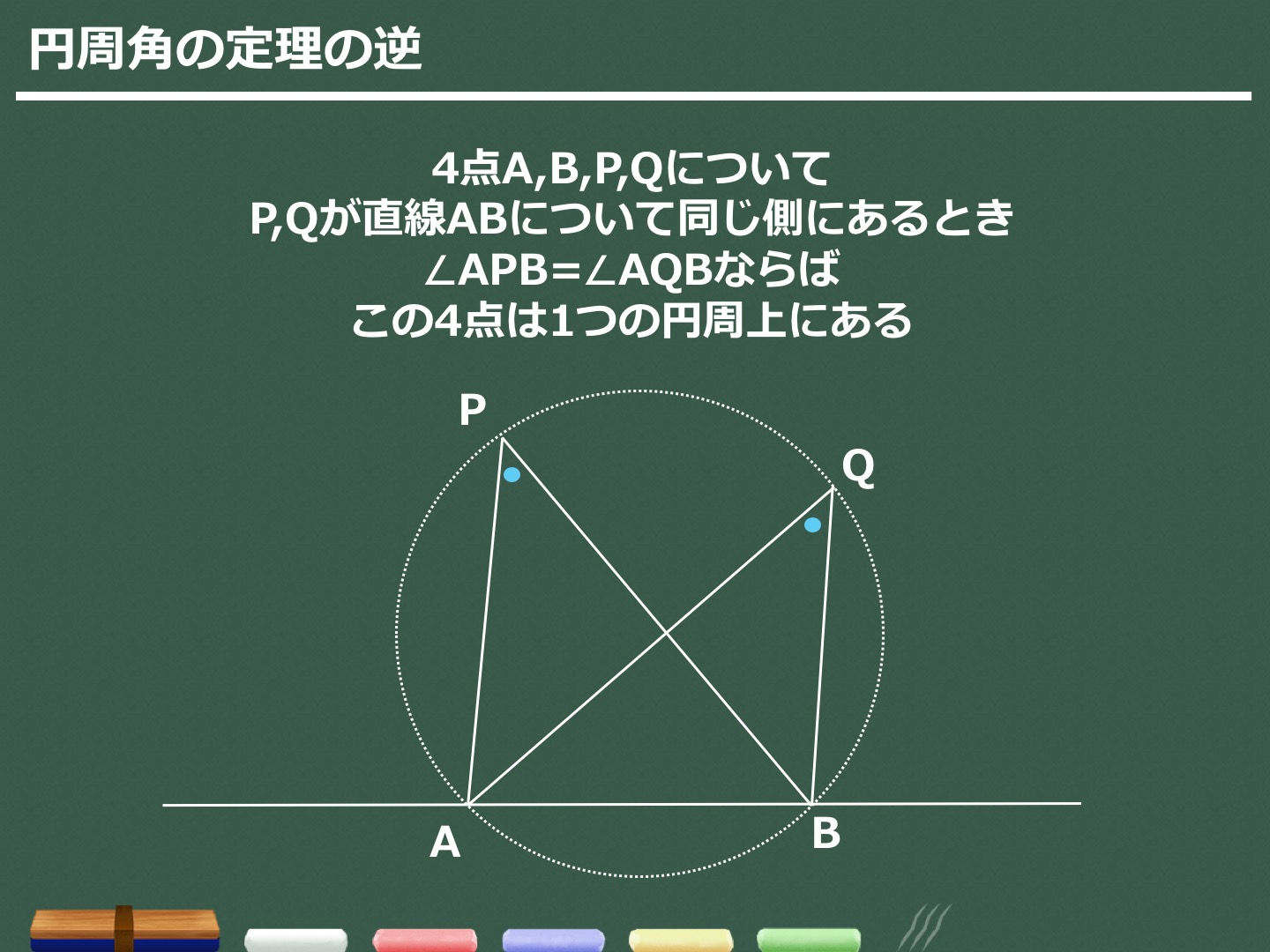


3分でわかる 円周角の定理とその逆の証明 問題の解き方 合格サプリ
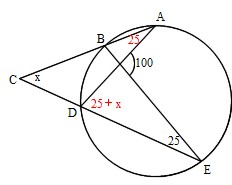


Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ


円周角の定理の証明



円周角 Wikipedia



円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学
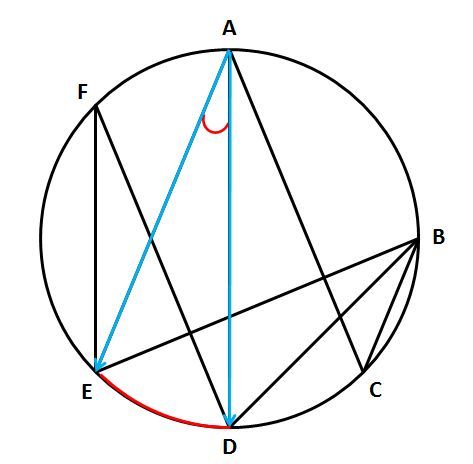


円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室



円と角度のチェックテスト2 円周角を求める発展問題 難しい問題もあります Youtube



円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ
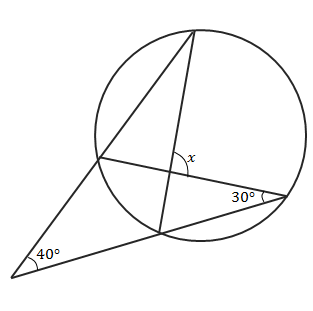


中3数学 円周角 ブーメラン型四角形 まとめと問題



この2つの問題の角xの部分の解き方と答えを教えてください Clear
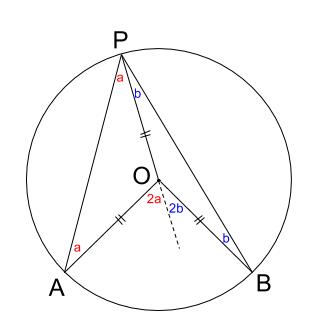


中学数学 円周角の定理はなぜ成り立つのか 中学数学の無料オンライン学習サイトchu Su


中学数学 円周角 中心角



円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ



高校数学 正弦定理 円周角の定理と三角比の融合 の証明と利用 受験の月


中学受験 図形の角度問題は 7つ道具 で攻略 かるび勉強部屋



中3数学 円周角の定理の逆 の重要ポイント 映像授業のtry It トライイット



円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ



数学 中3 56 円周角の定理 基本編 Youtube


円周角の定理 練習問題 苦手な数学を簡単に


中学数学 円周角 中心角
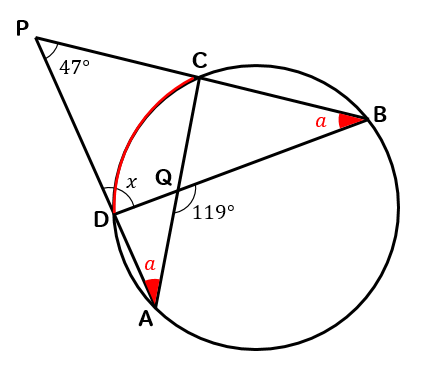


円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ
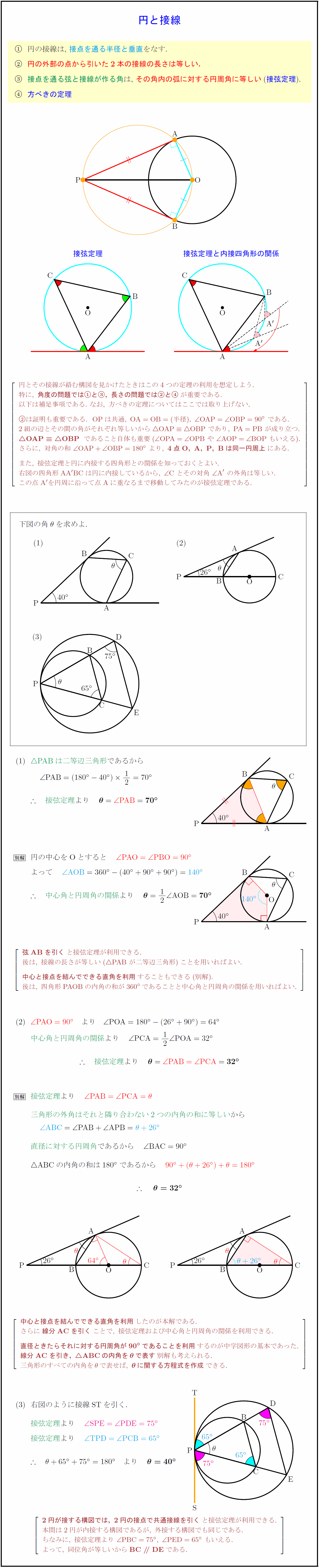


高校数学a 円と接線に関する3定理 垂直 接線の長さ 接弦定理 受験の月
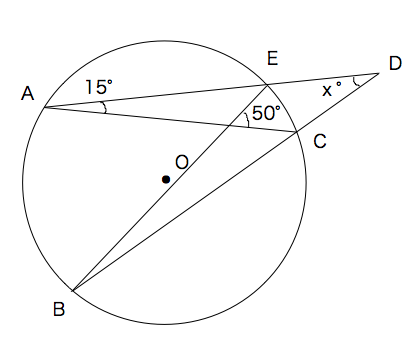


円周角の定理 練習問題 苦手な数学を簡単に


円周角と中心角 中学から数学だいすき
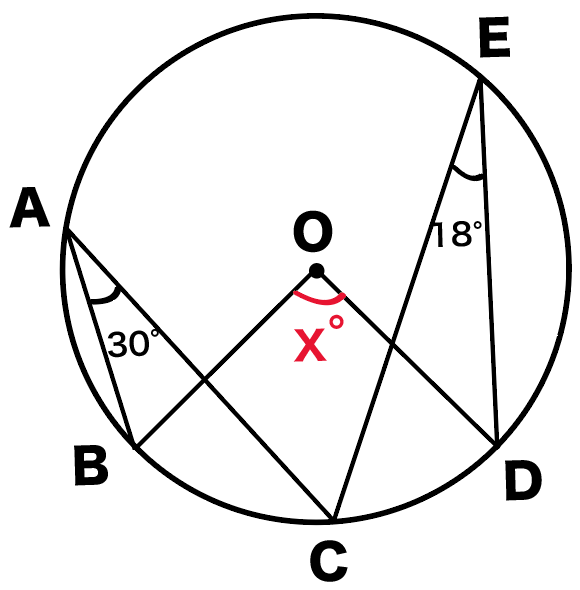


円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく



円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学


円周角



円周角の定理と証明 中心角の求め方を詳しく解説 Rikeinvest



円周角の定理を使って角度を求める問題の解き方 現役塾講師のわかりやすい中学数学の解き方



円周角と円の外の点を結んで おときち副塾長 電脳空間学習塾かもん Youtube


円と三角形 角度 中学から数学だいすき
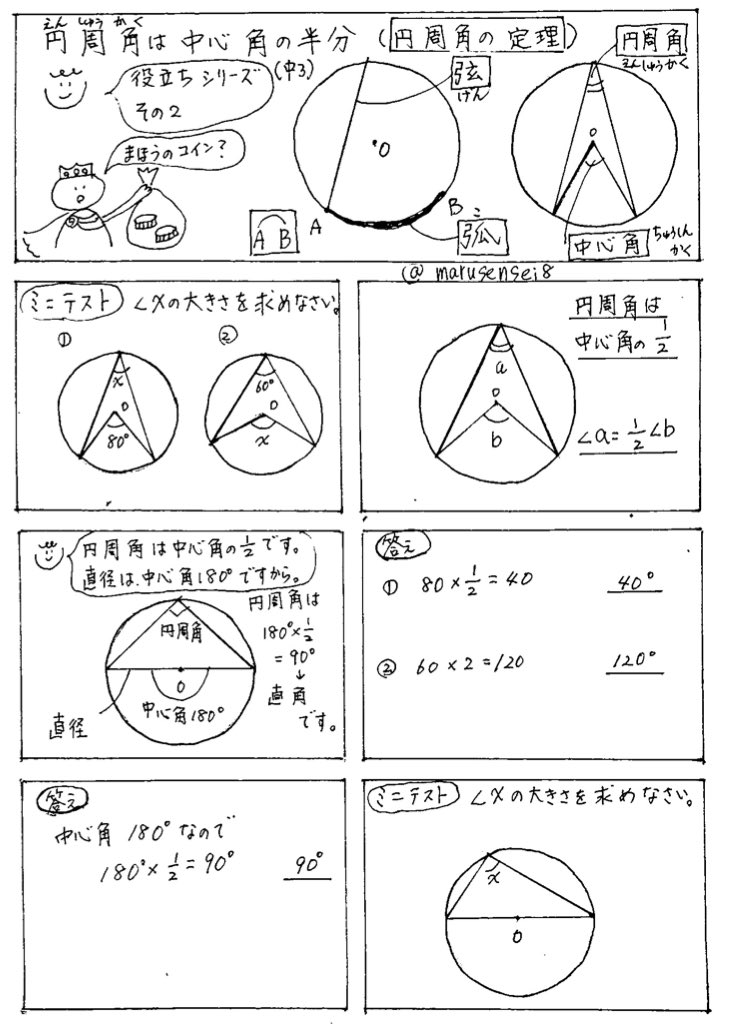


円周角



円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者


同じ弧に対する円周角
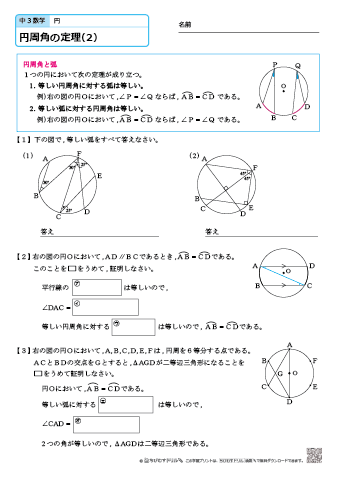


中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生



中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット


円周角
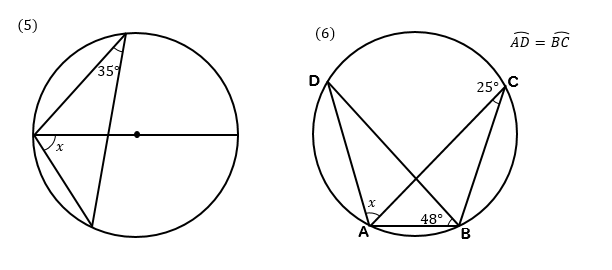


これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ



円周角の定理はこれで完璧 定理の証明と様々な問題の解法



円周角の定理 円周角と中心角の関係は中学や高校でよく出るぞ 中学や高校の数学の計算問題


円周角の定理とその逆 思考力を鍛える数学



円周角の解き方 中学数学に関する質問 勉強質問サイト



円周角の定理



数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア
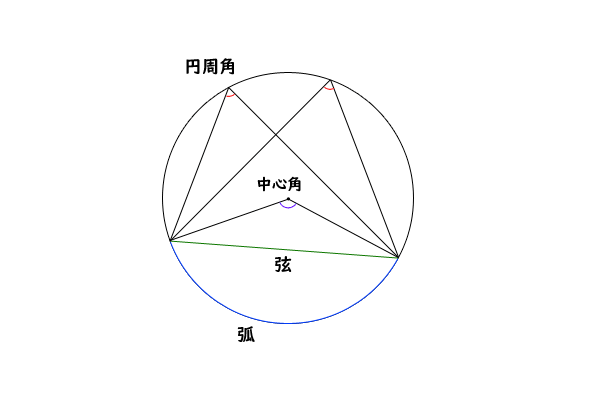


円周角の定理とその逆の証明 高校数学マスター
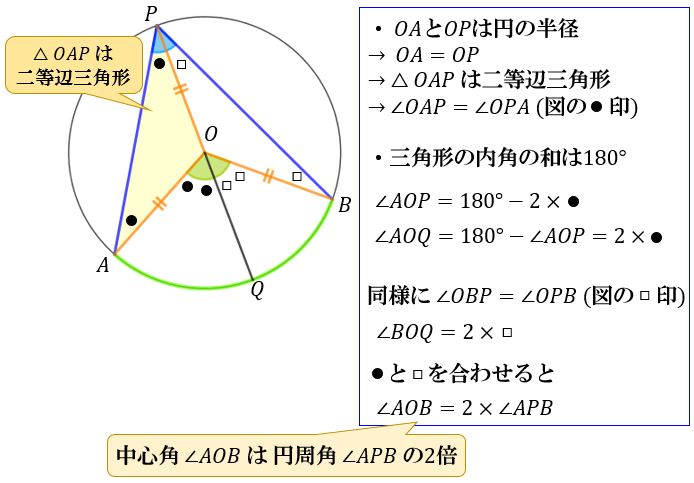


円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ
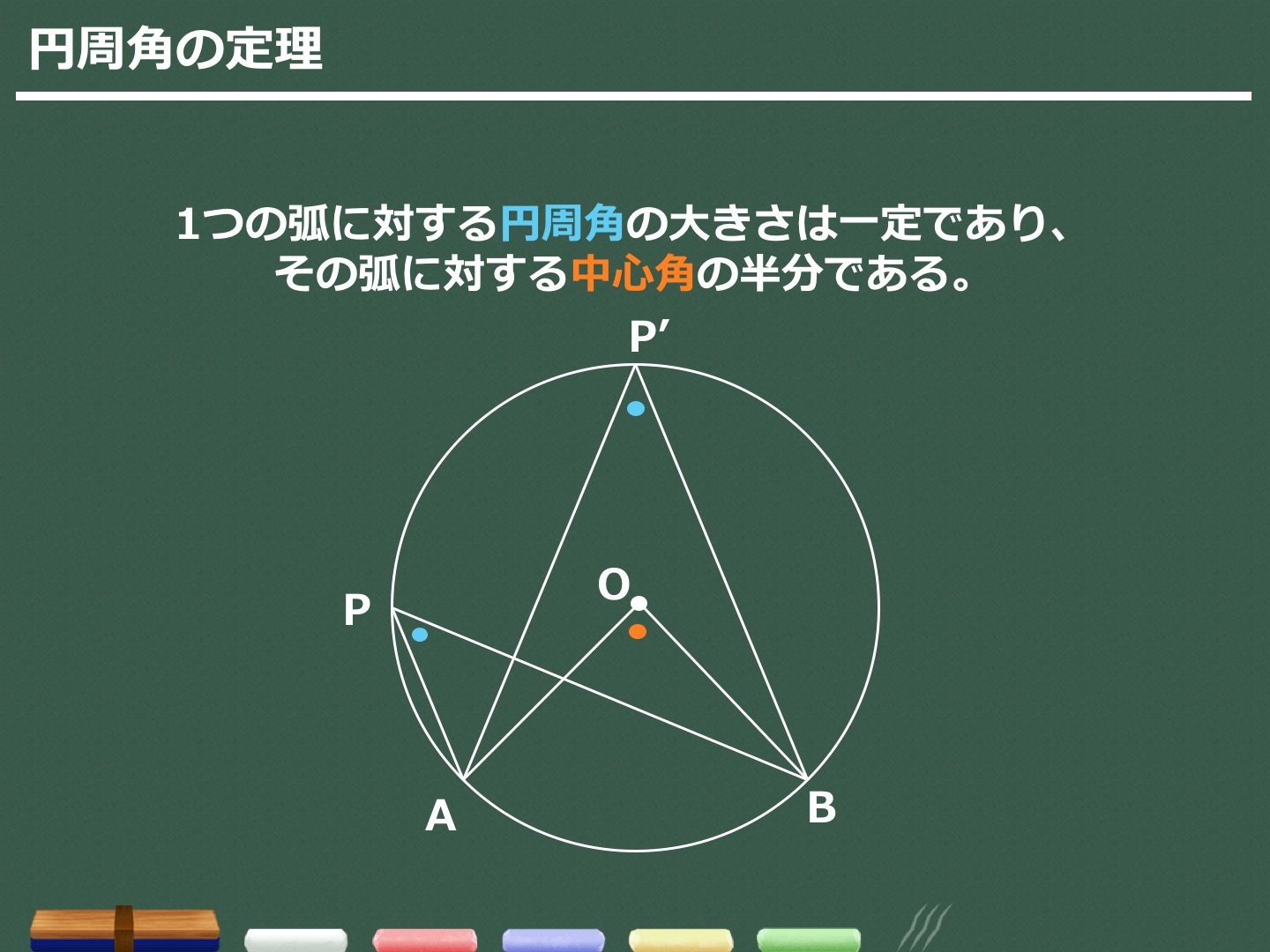


3分でわかる 円周角の定理とその逆の証明 問題の解き方 合格サプリ



円周角の定理 円に内接する四角形等図形の練習問題 中学 高校数学 身勝手な主張



円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者



中学数学 円周角 中心角
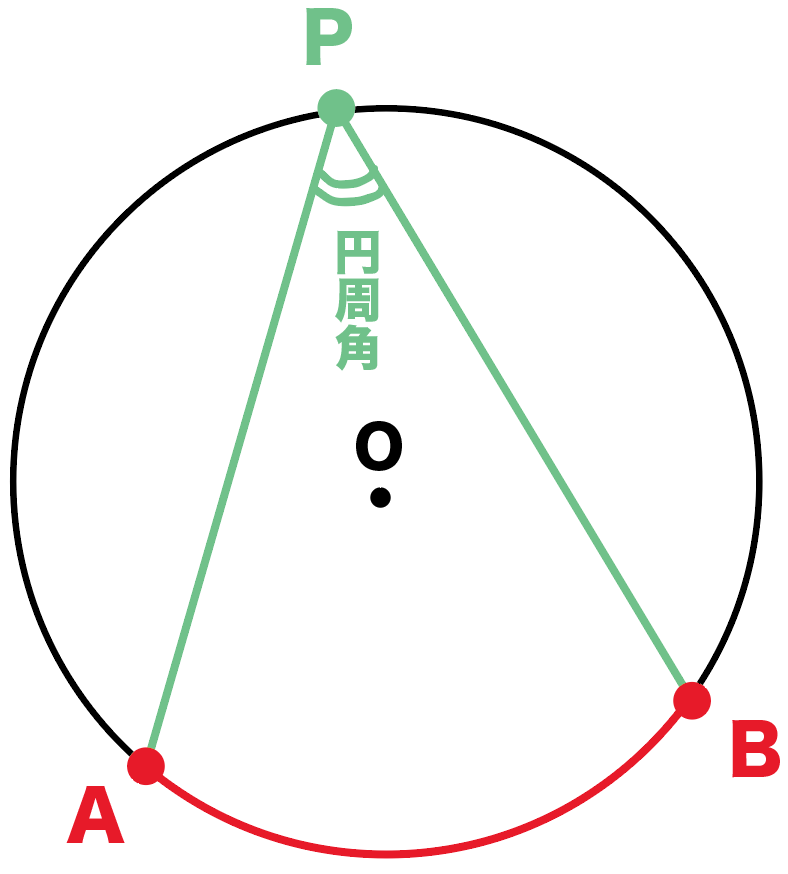


3分でわかる 円周角の定理とはなんだろう Qikeru 学びを楽しくわかりやすく



円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ
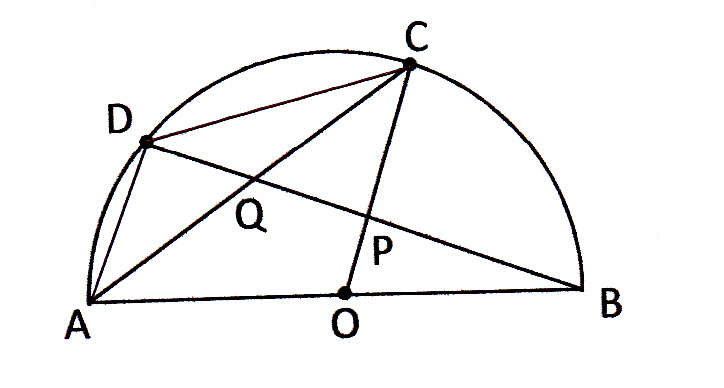


円周角の定理を使った相似の証明の解き方 現役塾講師のわかりやすい中学数学の解き方


円周角の定理
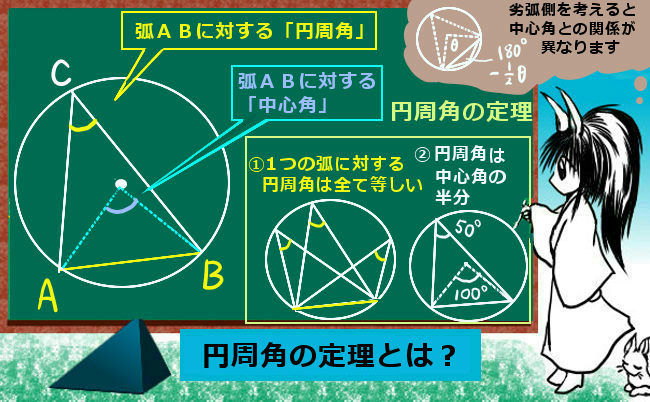


円周角の定理 理数系無料オンライン学習 Kori



中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット
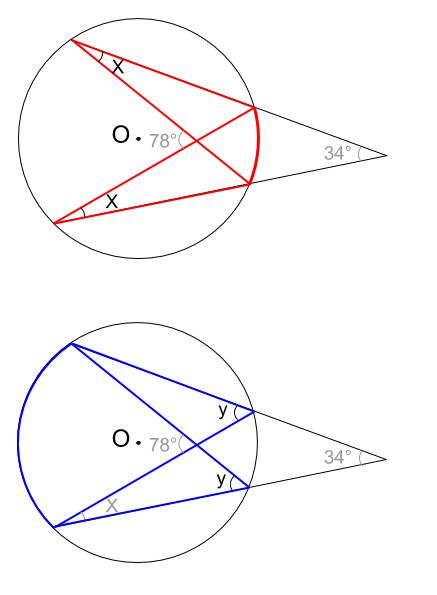


中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su



円周角と孤の比 中学数学に関する質問 勉強質問サイト
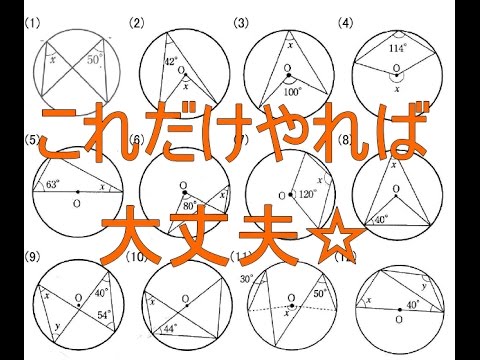


円周角の定理と中心角 中学3年数学 Youtube
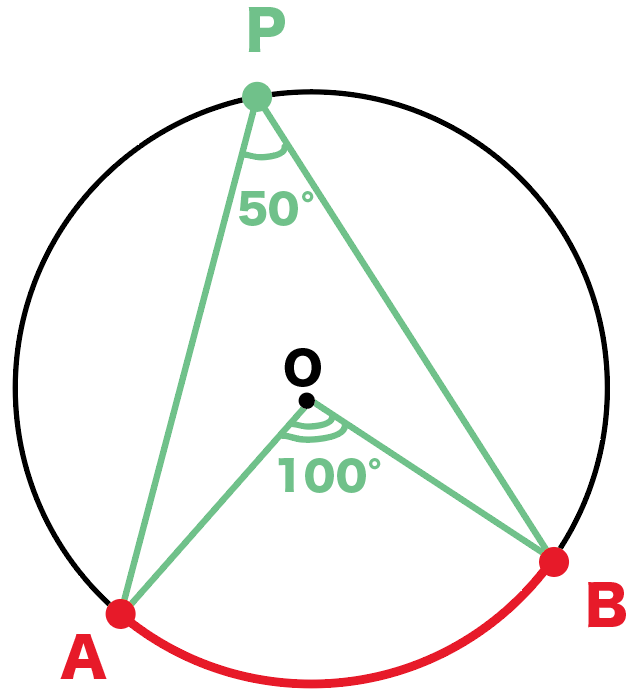


3分でわかる 円周角の定理とはなんだろう Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿